SIMULASI

A.    PENGERTIAN SIMULASI

          Simulasi berasal dari bahas Inggris, yaitu to simulate, yang artinya menurut Webster’s Collegiate Dictionary adalah “ to feign, to obtain the essence of without the reality “ untuk memperoleh intisari dari sesuatu tanpa melibatkan kenyataan. Sedangkan menurut Oxford American Dictionary ( 1980 ) simulasi adalah “ to reproduce the condition of a situasion, as by means of a model, for studi or testing or training, etc” untuk menghasilkan suatu kondisi dari sebuah situasi, dalam maksud sebuah model, untuk dipelajari atau untuk percobaan atau pelatihan, dan sebagainya.  

          Menurut Pusat Bahasa Depdiknas (2005) simulasi  adalah satu metode pelatihan yang memperagakan sesuatu dalam bentuk tiruan (imakan) yang mirip dengan keadaan yang sesungguhnya; simulasi: penggambaran suatu sistem atau proses dengan peragaan memakai model statistic atau pemeran.

          Simulasi adalah sebuah replikasi atau visualisasi dari perilaku sebuah sistem, misalnya sebuah perencanaan pendidikan, yang berjalan pada kurun waktu yang tertentu. Jadi dapat dikatakan bahwa simulasi itu adalah sebuah model yang berisi seperangkat variabel yang menampilkan ciri utama dari sistem kehidupan yang sebenarnya. Simulasi memungkinkan keputusan-keputusan yang menentukan bagaimana ciri-ciri utama itu bisa dimodifikasi secara nyata.

Kelebihan Simulasi

1.    Simulasi dapat memberi jawaban yang tidak bisa dilakukan model analitik

2.    Simulasi dapat digunakan untuk analisis yang besar dan komplek pada situasi keadaan nyata yang tidak dapat dilakukan oleh model kuantitatif konvensional

3.    Model simulasi lebih realistis terhadap sistem nyata karena asumsi yang lebih sedikit

4.    Simulasi membolehkan kita untuk mempelajari pengaruh alternatif dari kumpulan individu atau variabel mana yang lebih penting

5.    Pada banyak hal, simulasi lebih murah dari percobaannya sendiri.

6.    Untuk sejumlah proses dimensi, simulasi memberikan penyelidikan yang langsung dan terperinci dalam periode waktu khusus.

 Kekurangan Simulasi

1.    Simulasi bukan presisi dan juga bukan suatu proses optimasi. Simulasi tidak menghasilkan penyelesaian, tetapi menghasilkan cara untuk menilai jawaban termasuk jawaban optimal.

2.    Model Simulasi yang baik dan efektif  adalah sangat mahal dan membutuhkan waktu yang lama dibandingkan dengan model analitik

3.    Tidak semua situasi dapat dinilai melalui simulasi kecuali situasi yang memuat ketidakpastian (probability)

         

B.     JENIS-JENIS SIMULASI

Klasifikasi atau pengelompokan dari teknik simulasi dibagi menjadi 3 kelompok ( Law & Kelton,2000 ), yaitu

1.    Model Simulasi Statis dan Dinamis

     Simulasi Statis merupakan representasi dari sebuah system pada suatu tertentu, atau digunakan pada system dimana waktu tidak mempunyai peran. Penerapan paling sederhana pada simulasi ini adalah saat kita memasukan nilai variable pada suatu rumus untuk memperoleh hasil akhirnya. Contoh lain dari simulasi statis adalah Model Monte Carlo. Dilain pihak, simulasi dinamis mewakili system yang berubah-ubah menurut waktu, misalnya system ban berjalan pada pabrik atau sirkulasi parker.

2.    Model Simulasi Deterministik dan Model Simulasi Stochastic

     Bila system simulasi tidak mempunyai komponen probabilitas ( kemungkinan ), maka dinamakan simulasi deterministic. Contoh dari system ini adalah persamaan diferensial yang menghitung reaksi kimia. Hasil akhir dari simulasi deterministic telah ditentukan ketika sejumlah input dimasukan kedalam model, walaupun bisa saja diperlukan waktu yang lama untuk menghitung hasil akhir simulasi tersebut.

     Bila system tersebut memiliki beberapa komponen input acak ( random ), maka simulasi tersebut termasuk simulasi stochastic. Hasil akhir atau keluaran dari model stochostik ini berupa komponen acak. Kebanyakan system antrian ( queueing ) dan persediaan ( inventory ) merupakan model stochostik.

3.    Model Simulasi Kontinyu dan Model Simulasi Diskrit

     Simulasi kontinyu merupakan model system yang kondisi status variablenya berubah-ubah terus menerus sesuai dengan waktu. Simulasi model ini melibatkan persamaan diferensial yang merupakan relasi dari tingkat populasi penduduk pada suatu daerah dengan memperhatikan fertilitas dan moralitas. Contoh

       

C.    SIMULASI MONTE CARLO

          Simulasi Monte Carlo merupakan suatu pendekatan untuk membentuk kembali distribusi peluang yang didasarkan pada pilihan atau pengadaan bilangan acak (random).

          Istilah Monte Carlo sering dianggap sama dengan simulasi probabilistik. Namun Monte Carlo Sampling secara lebih tegas berarti teknik memilih angka secara acak dari distribusi probabilitas untuk menjalankan simulasi. Dasar dari simulasi Monte Carlo adalah percobaan elemen kemungkinan dengan menggunakan sampel random (acak). Metode ini terbagi dalam 5 tahapan:

1.    Membuat distribusi kemungkinan untuk variabel penting

2.    Membangun distribusi kemungkinan kumulatif untuk tiap‐tiap variabel di tahap pertama

3.    Menentukan interval angka random untuk tiap variabel

4.    Membuat angka random

5.    Membuat simulasi dari rangkaian percobaan

Penjelasan dari ke 5 tahapan tersebut adalah sebagai berikut:

1.    Membuat Distribusi Kemungkinan untuk Variabel Penting

Gagasan dasar dari simulasi monte carlo adalah membuat nilai dari tiap variabel yang merupakan bagian dari model yang dipelajari. Banyak variabel di dunia nyata yang secara alami mempunyai berbagai kemungkinan yang mungkin ingin kita simulasikan.

Salah satu cara umum untuk membuat distribusi kemungkinan untuk suatu variabel adalah memperhitungkan hasil di masa lalu. Kemungkinan atau frekuensi relative untuk tiap kemungkinan hasil dari tiap variabel ditentukan dengan membagi frekuensi observasi dengan jumlah total observasi

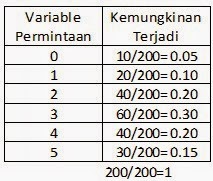
Contoh: Permintaan akan Shinpo Container Box 52L pada LotteMart Indonesia Cabang Ratu Plaza  selama 200 hari kebelakang terlihat di tabel berikut:

Tabel 1

    Kita dapat merubah keadaan tersebut diatas menjadi distribusi kemungkinan (bila kita asumsikan tingkat penjuala dimasa lalu akan tetap bertahan sampai ke masa depan) dengan membagi tiap permintaan dengan total permintaan. Seperti pada tabel berikut:

Tabel 2.

2.  Membangun Distribusi Kemungkinan Kumulatif untuk Tiap‐Tiap Variabel di Tahap Pertama

     Konversi dari distribusi kemungkinan biasa, seperti pada kolom kanan tabel 2 menjadi distribusi kumulatif dilakukan dengan menjumlahkan tiap angka kemungkinan dengan jumlah sebelumnya seperti pada tabel 3.

Tabel 3.

    Probabilitas kumulatif terlihat pada gambar dibawah, digunakan pada tahap ke 3 untuk membantu menempatkan nilai random

3.    Menentukan Interval Angka Random untuk Tiap Variabl

    Setelah kita menentukan probabilitas kumulatif untuk tiap variabel yan termasuk dalam simulasi, kita harus menentukan batas angka yang mewakili tiap kemungkinan hasil. hal tersebut ditujukan pada interval angka random. Penentuan interval didasari oleh kemungkinan kumulatif

Tabel 4.

Interval Angka Random

4.    Membuat Angka Random

   Untuk membuat angka random kita bisa menggunakan software Microsoft Excel dengan menggunakan perintah Randbetween, misal untuk angka random dari 1‐ 100, kita tuliskan perintah: =randbetween(1,100) dan diulangi sejumlah baris yang diperlukan

5.    Membuat Simulasi dari Rangkaian Percobaan

     Kita bisa membuat simulasi dari sebuah eksperimen dengan mengambil angka random dari gambar diatas, misal kita akan membuat simulasi untuk 10 hari, kita ambil Kolom A1‐ A10. Cara penentuan permintaan adalah dengan ditentukan oleh angka random. Contohnya bila angka random adalah 56, angka itu terletak pada interval 36 s/d 65 yang berarti permintaan 3 buah ban.

Tabel 5. 

Total permintaan untuk 10 hari adalah 28 ban, rata‐rata permintaan per hari adalah 2,8 ban

Ada beberapa dasar-dasar dalam teori simulasi metode Monte Carlo diantaranya :

a. Variable Random

b. Distribusi Biominal

c. Distribusi Normal

d. Distribusi Normal Multivarirat

e. Fungsi Lagrange

f. Uji Lilliefors untuk Kenormalan

g. Matriks

h. Pembangkit Bilangan Random

                Metode Simulasi Monte Carlo adalah suatu metode untuk mengevaluasi suatu model deterministik yang melibatkan bilangan acak sebagai salah satu input. Metode ini sering digunakan jika model yang digunakan cukup kompleks, non linear atau melibatkan lebih dari sepasang parameter tidak pasti. Sebuah simulasi Monte Carlo dapat melibatkan 10.000 evaluasi atas sebuah model, suatu pekerjaan di masa lalu hanya bisa dikerjakan oleh sebuah software komputer. Suatu model memerlukan parameter input dan beberapa persamaan yang digunakan untuk menghasilkan output (atau variabel respon). Dengan menggunakan parameter input berupa bilangan random, maka dapat mengubah suatu model deterministik menjadi model stokastik, dimana model deterministik merupakan suatu model pendekatan yang diketahui dengan pasti sedangkan model stokastik tidak pasti.

 Simulasi Monte Carlo adalah metode untuk menganalisa perambatan ketidakpastian dimana tujuannya adalah untuk menentukan bagaimana variasi random atau error mempengaruhi sensitivitas, performa atau reliabilitas dari sistem yang sedang dimodelkan. Simulasi Monte Carlo digolongkan sebagai metode sampling karena input dibangkitkan secara random dari suatu distribusi probabilitas untuk proses sampling dari suatu populasi nyata. Oleh karena itu, suatu model harus memilih suatu distribusi input yang paling mendekati data yang dimiliki (Rubinstein, 1981)

Oleh :

Ahmad Hadi Assari

Riadi

M. Zaenal Mukhlasin

Qolbi Latamaro Imanullaoh

4EA16